Velkaencyklopedie - Vše, co potřebujete do školy

Obor přirozených čísel

1,2,3…

-          Značka N

-          Platí že:

·         A + B = B + A

·         A • B = B • A

·         => K – KONUTATIVNOST

·         A + (B + C) = (A + B) + C

·         A • (B • C) = (A • B) • C

·         => A – ASOCIATIVNOST

·         A • (B + C) = AB + AC

·         => D – DISTRIBUTIVNOST

·         A • 1 = A

·         => NEUTRALITA

Obor celých čísel

… -4, -3, -2, -1, 0, 1, 2, 3 …

-          Značka Z

-          Platí totéž co u N a navíc:

·         A + 0 = A

·         => N – neutralita

Obor racionálních čísel

… -2; -1,5; 0 ; 2/5, 8 …

-          Značka Q

-          Jsou to čísla, která nelze zapsat ve tvaru p/q, kde p je Z a Q je N

-          Pokud p a q nemá společného dělitele kromě 1 (jsou nesoudělná), pak zlomek je zlomek v základním tvaru

Obor reálných čísel

… -2; -1,5; 0; 2/5; 8; √2; √8, √3…

-          Značka R

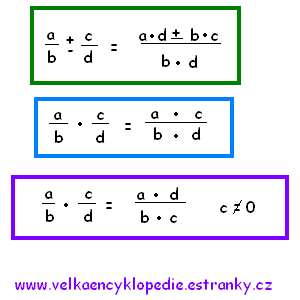
-          Pro každé 2 R čísla a/b a c/d platí:

-           

ČÍSLA LZE ZAPSAT:

1. Desetinným číslem

2. Zlomkem

3. Periodickým číslem

·         1. Ryze periodická                             __

o   10/33 = 10:33 = 0,30303 => 0,30

·         2. Neryze periodická                            __

o   15/22 = 15:22 = 0,681818 => 0,681 perioda

                               Před perioda