Trojúhelníky
1. Trojúhelník různostranný
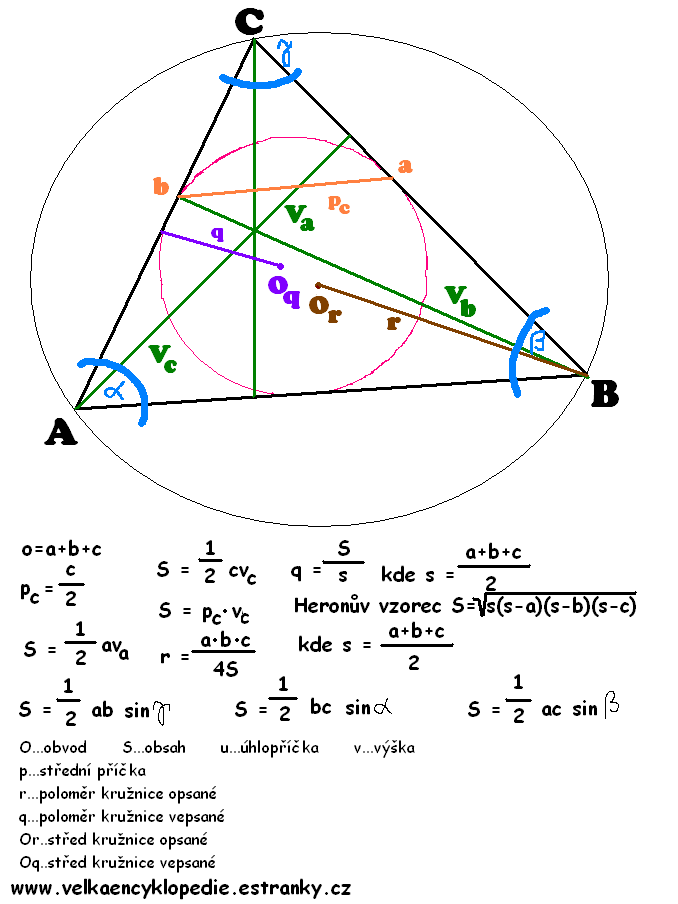
2. Trojúhelník pravoúhlý
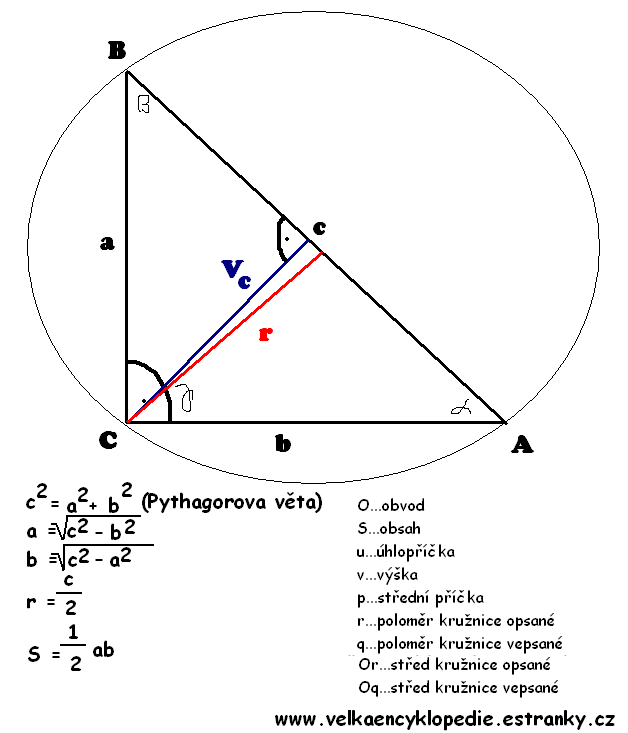
3. Trojúhelník rovnoramenný
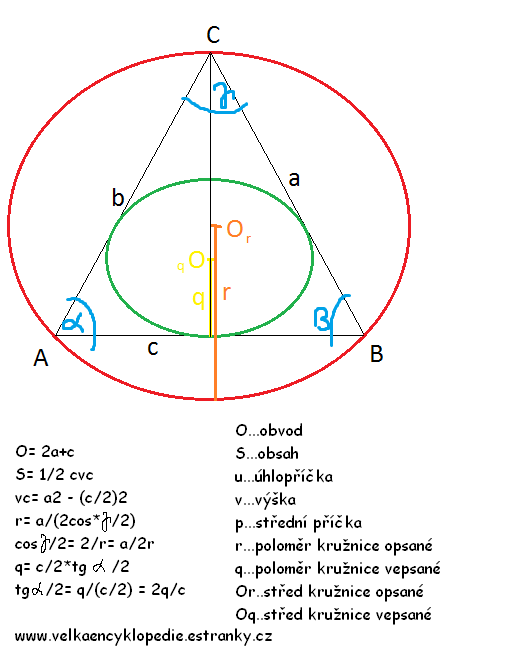
4. Trojúhelník rovnostranný
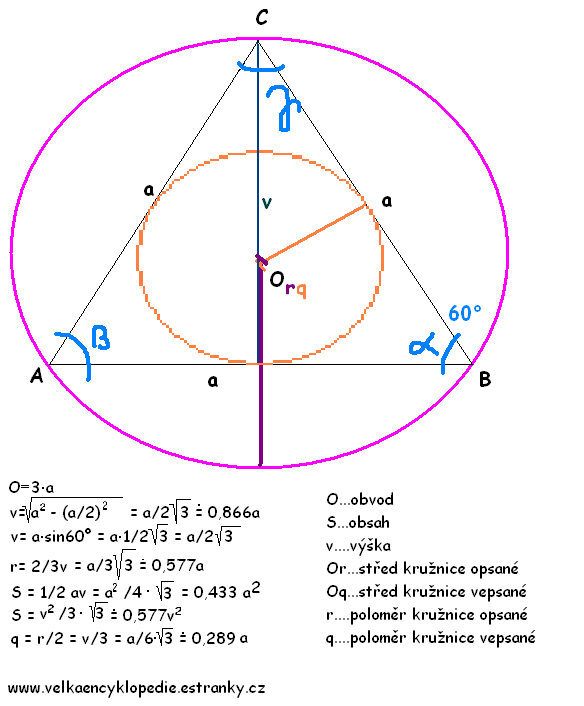
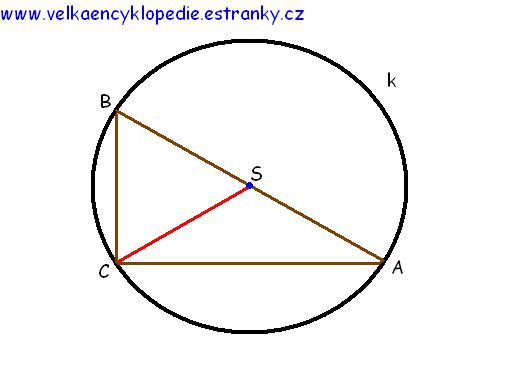
5. Thaletova věta
- pro libovolný trojúhelník ABC platí:
- jestliže je ABC pravoúhlý trojúhelník s přeponou AB, leží vrchol C na kružnici k s průměrem AB
- jestliže je vrchol C leží na kružnici k s průměrem Ab je ABC pravoúhlý trojúhelník s přeponou AB
- kružnice k je Thaletova kružnice s průměrem AB
Všechny trojúhelníky, jejichž střed kružnice opsané půlí nejdelší stranu, jsou pravoúhlé
6. Věty o shodnosti
- Věta SSS
- Dva trojúhelníky se shodují ve všech třech stranách, jsou shodné
- Věta SUS
- Dva trojúhelníky se shodují ve dvou stranách a úhlu těmito stranami sevřený, jsou shodné
- Věta USU
- Dva trojúhelníky se shodují v jedné straně a obou úhlech k této straně přilehlých, jsou shodné
- Věta SSU
- shodují-li se 2 trojúhelníky ve 2 stranách a úhlu proti větší z nich, jsou shodné
7. Podobnost
- 2 útvary jsou podobné, mají-li vzdálenosti odpovídající si bodů stejný poměr
k (poměr podobnosti) = A'B' / AB = B'C' / BC = A'C' / AC
k > 1 ... nový útvar je zvětšený
0 < k < 1 ... nový útvar je zmenšený
k = 1 ... ptvar je stejně velký -> shodnost
- každé 2 čtverce jsou podobné, každé 2 kružnice jsou podobné, každé 2 rovnostranné trojúhelníky jsou podobné
- Věta SSS
- dva trojúhelníky mají stejné poměry, každý dvou odpovídajících si stran jsou podobné
- Věta SUS
- každé 2 trojúhelníky, které mají stejné poměry délek 2 odpovídajích si stran a shodují se v úhlu jimi sevřeném, jsou podobné
- Věta UU
- Každé 2 trojúhelníky, které se shodují ve 2 úhlech jsou si posobné
8. Stejnolehlost
- Jde o druh podobného zobrazení
- v rovině je dán bod S a reálné číslo κ (kappa) , které je různé od 0 a od 1. každému bodu x roviny je přiřazen bod x' takto:
a) je-li x =S, pak x'= S (samodružný bod)
b) je-li x ≠ pak I X'S I = κ I XS I
- je-li κ > 0, pak x' leží na polopřímce SX
- je-li κ < 0, pak x' leží na polopřímce opačné k SX
- S - střed stejnolehlosti, κ - koeficient stejnolehlosti
9. Zápis konstrukčních úloh
a) Rozbor
- náčrtek + některé informace z konstrukce
- načrtneme jak bude trojúhelník po narýsování vypadat
- zadané údaje zvýrazníme tučně, barevně
b) Zápis
- postup konstrukce
- např. SSS
- I. AB ; I AB I = 32mm (sestrojíme úsečku AB o délce 32mm)
- II. k ; k (A ; r = 25mm) (sestrojíme kružnici k se středem v bodě A a poloměrem 25mm)
- III. l ; l (B ; r = 20mm) (sestrojíme kružnici l se středem v bodě B a poloměrem 20mm)
- IV. C ; C <- k n l (sestrojíme bod C jako průnik kružnic k a l)
- V. sestrojíme trojúhelník ABC
- např. SUS
- I. BC ; I BC I = 5cm (sestrojíme základnu BC o délce 5cm)
- II. úhel BCX ; I BCX I = 75° (sestrojíme úhel BCX o velikosti 75°)
- III. k ; k ( C ; r = 7cm) (z bodu C sestrojíme kružnici o poloměru 7cm)
- IV. A ; A <- k n CX (označíme bod A, který se nachází v průniku kružnice k a přímky CX)
- V. trojúhelník ABC
c) Konstrukce - zde narýsujeme
d) Rozbor řešení - Úloha má 1 (2,3 nebo více pokud je možno) řešení.
Komentáře
Přehled komentářů
Tato stránka se mi líbí, ale chtěla bych poprosit, jestli byste tady nepřidali také zápis k Thaletově větě krok po kroku, někteří učitelé po nás žádají podrobný zápis o popisu konstrukce. Velmi děkuji. :)

komentář
(Žákině, 16. 9. 2014 18:34)